Research

Grokking, the abrupt transition from memorization to generalisation after extended training, suggests the presence of competing solution basins with distinct statistical properties. We study this phenomenon through the lens of Singular Learning Theory (SLT), a Bayesian framework that characterizes the geometry of the loss landscape. The key measure is local learning coefficient (LLC) which quantifies the local degeneracy of the loss surface. SLT links lower-LLC basins to higher posterior mass concentration and lower expected generalisation error. Leveraging SLT, we develop a basin-selection perspective on grokking in quadratic networks: LLC ranks competing near-zero-loss basins by statistical preference, while the training-time transition between them is governed by optimisation dynamics. We derive closed-form expressions for the LLC in quadratic networks trained on modular arithmetic tasks. Empirically, we demonstrate that LLC trajectories estimated from training data track the onset of generalization and provide an informative probe of the optimisation path.

Joint work with Ben Cullen, Sergio Estan-Ruiz, and Riya Danait. [Paper]

In this paper, we study discrete Lyapunov models, which consist of steady-state distributions of first-order vector autoregressive models. The parameter matrix of such a model encodes a directed graph whose vertices correspond to the components of the random vector. This combinatorial framework naturally allows for cycles in the graph structure. We focus on the fundamental problem of identifying the entries of the parameter matrix. In contrast to the classical setting, we assume non-Gaussian error terms, which allows us to use the higher-order cumulants of the model. In this setup, we show generic identifiability for directed acyclic graphs with self-loops at each vertex and show how to express the parameters as a rational function of the cumulants. Furthermore, we establish local identifiability for all directed graphs containing self loops at each vertex and no isolated vertices. Finally, we provide first results on the defining equations of the models, showing model equivalence for certain graphs and paving the way towards structure learning

Joint work with Cecilie Olesen Recke, Sarah Lumpp, Nataliia Kushnerchuk, Janike Oldekop, Jane Ivy Coons, and Elina Robeva. [Paper]

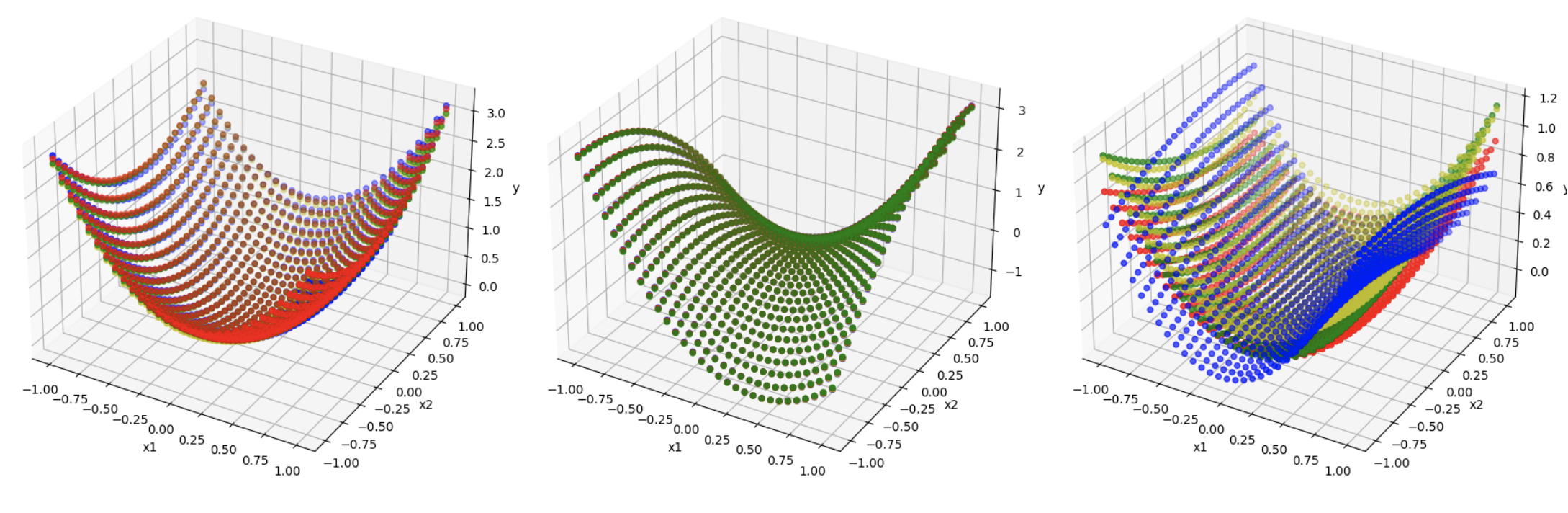
In this paper, we study the expressivity and learning process for polynomial neural networks (PNNs) with monomial activation functions. The weights of the network parametrize the neuromanifold. In this paper, we study certain neuromanifolds using tools from algebraic geometry: we give explicit descriptions as semialgebraic sets and characterize their Zariski closures, called neurovarieties. We study their dimension and associate an algebraic degree, the learning degree, to the neurovariety. The dimension serves as a geometric measure for the expressivity of the network, the learning degree is a measure for the complexity of training the network and provides upper bounds on the number of learnable functions. These theoretical results are accompanied with experiments.

Joint work with Kaie Kubjas and Maximilian Wiesmann. [Paper]

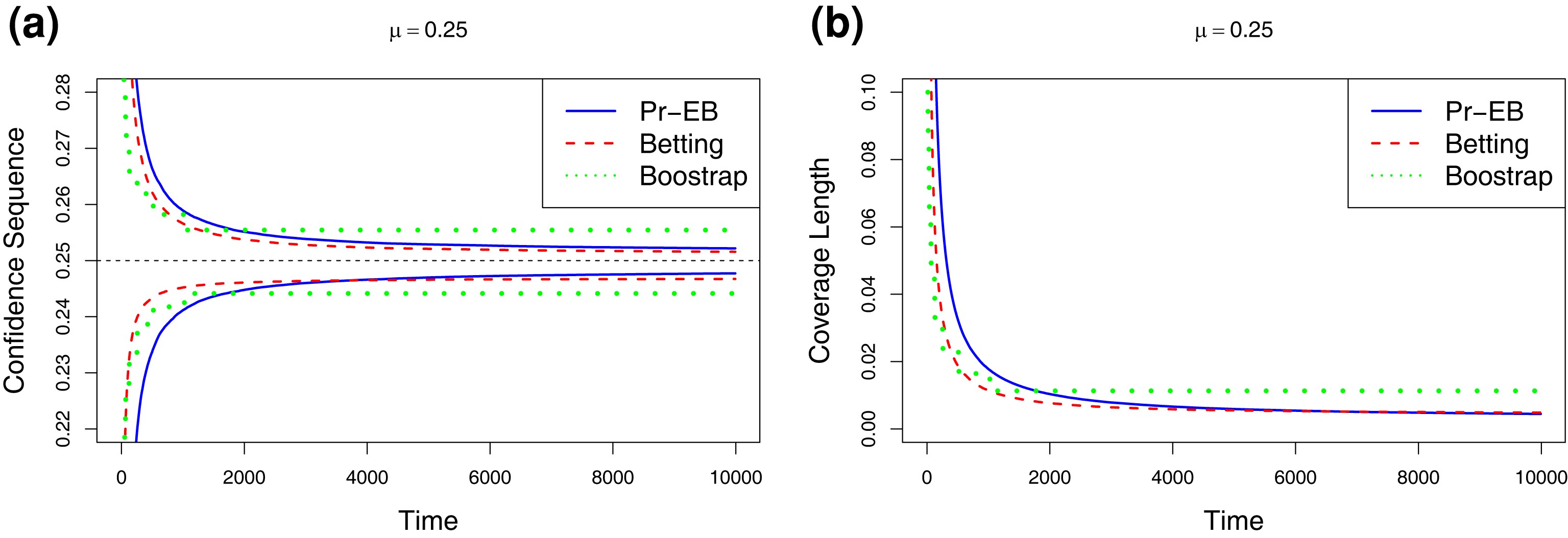
In this work, we evaluate the betting method proposed by Waudby-Smith and Ramdas in generating confidence intervals and time-uniform confidence sequences for mean estimation with bounded observations. The methodology utilises composite non-negative martingales and establishes a connection to game-theoretic probability. We perform numerical comparisons with alternative methods and propose extension to vector settings.

Joint work with Yuantong Li and Xianwu Dai. [Paper]

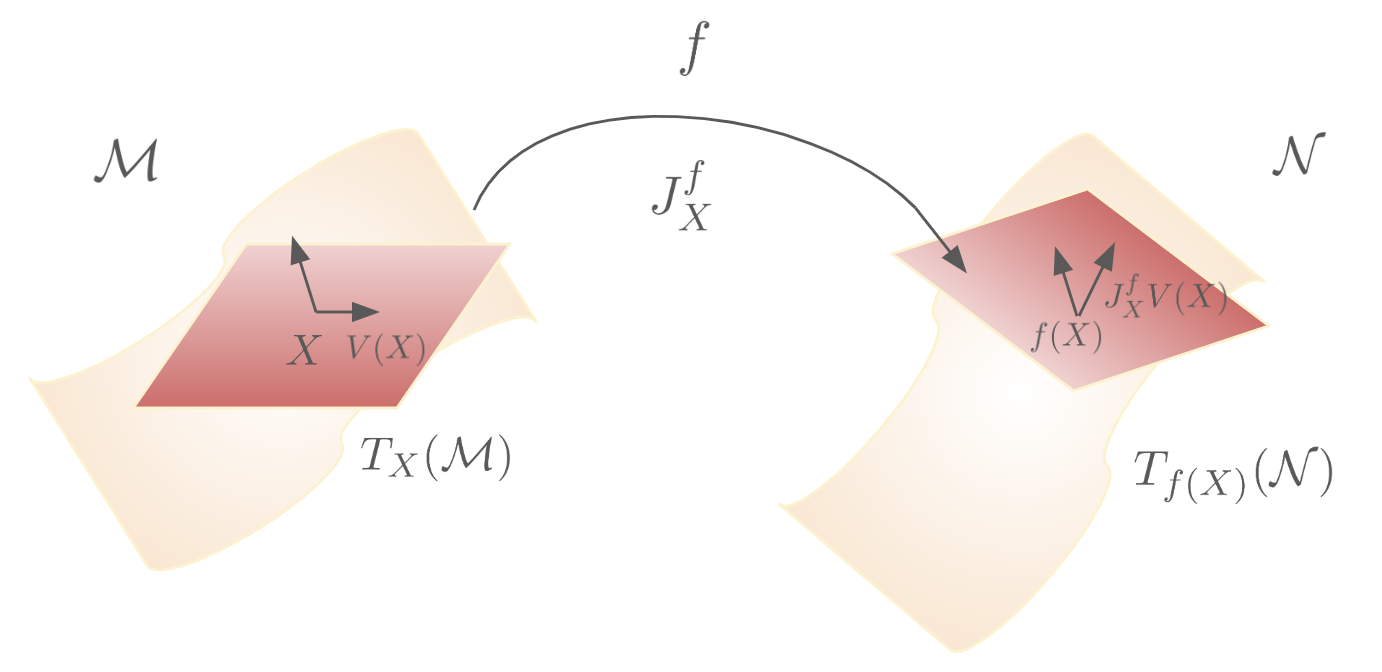
This paper investigates the spectrum of the Jacobian of PH data encodings and the pull-back geometry that they induce on the data manifold. Then, by measuring different perturbations and features on the data manifold with respect to this geometry, we can identify which of them are recognized or ignored by the PH encodings. This also allows us to compare different encodings in terms of their induced geometry. Importantly, the approach does not require training and testing on a particular task and permits a direct exploration of PH. We experimentally demonstrate that the pull-back norm can be used as a predictor of performance on downstream tasks and to select suitable PH encodings accordingly. All experiments were conducted by the first author; I worked with formulating the pull-back norm and the differential geometry background.

Joint work with Shuang Liang, Renata Turkeš, Nina Otter and Guido Montúfar. [Paper]

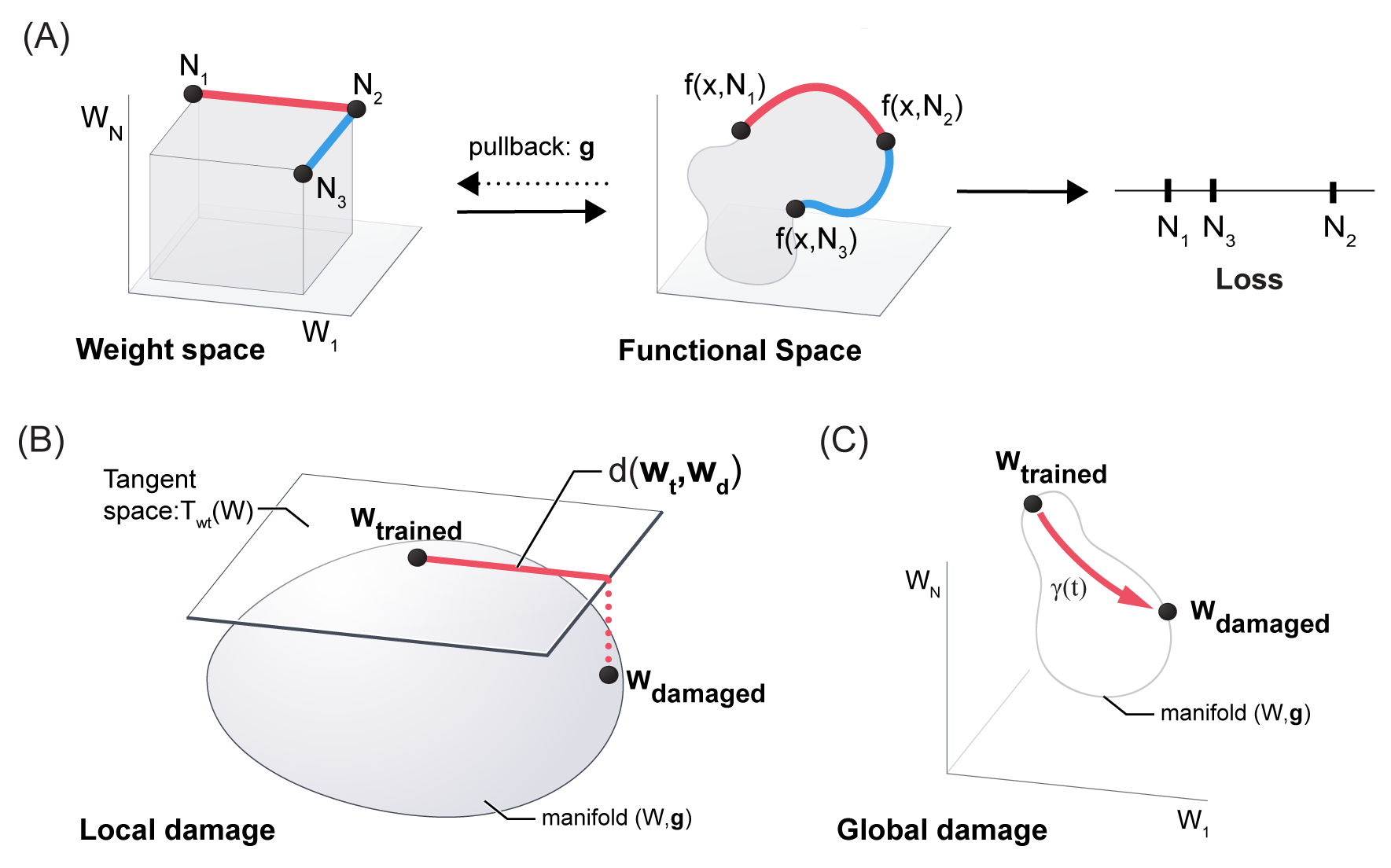
In this paper, we establish a mathematical framework to analyze the resilience of artificial neural networks through the lens of differential geometry. Our geometric language provides natural algorithms that identify local vulnerabilities in trained networks as well as recovery algorithms that dynamically adjust networks to compensate for damage. We reveal striking vulnerabilities in commonly used image analysis networks, like MLP's and CNN's trained on MNIST and CIFAR10 respectively. We also uncover high-performance recovery paths that enable the same networks to dynamically re-adjust their parameters to compensate for damage. Broadly, our work provides procedures that endow artificial systems with resilience and rapid-recovery routines to enhance their integration with IoT devices as well as enable their deployment for critical applications.

Joint work with Guruprasad Raghavan and Matt Thomson. [paper]

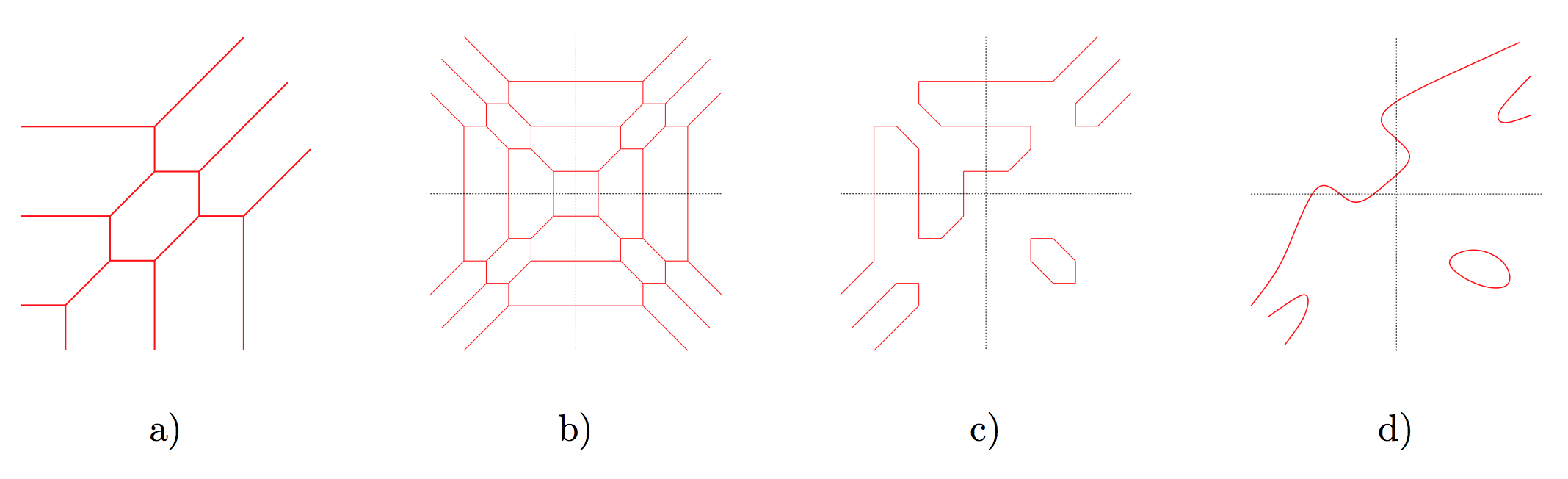
Tropical geometry is a variant of algebraic geometry where people study polynomials and their geometric properties with addition replaced by minimization and multiplication replaced by ordinary addition. Under this formulation, the polynomial graphs would resemble piecewise linear meshes where numbers belong to the tropical semiring instead of a field. The maximum operation and the piecewise linear property of the mesh leads us to think of neural networks with a particular family of activations and the linear regions cut out by the activation functions. In 2018, Zhang et al. established the first connection between tropical geometry and feedforward neural networks with ReLU activation by showing that the family of such neural networks is equivalent to the family of tropical rational maps. We generalized the results from Zhang's paper and applied other techniques such as patchworking to study the expressive power of neural networks with piecewise linear activation functions.

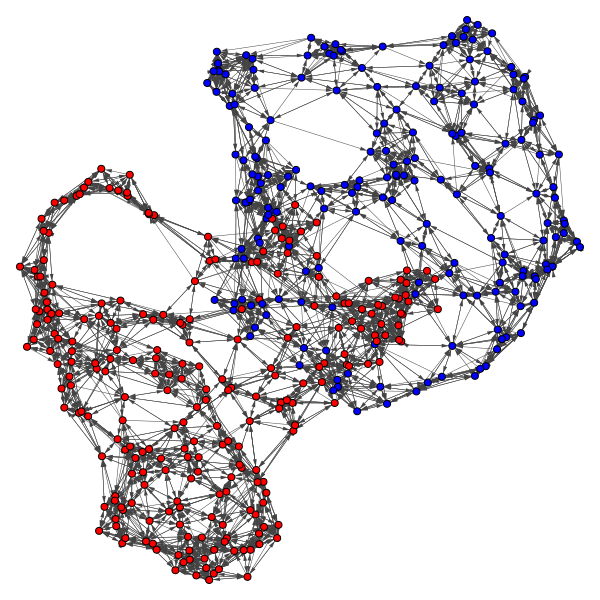
We utilize voting records in conjunction with clustering and community detection algorithms to classify legislators into communities by political stance. The underlying assumption is that legislators with more similar voting records have more similar political stances. We consider legislatures from multiple countries: the United States House of Representatives, German Bundestag, Legislative Council of Hong Kong, and South Korean National Assembly. For each legislature, we collect roll call voting data and apply five different similarity functions to construct similarity matrices of the legislators. We then apply spectral clustering, Louvain with and without k-nearest neighbors preprocessing, and MBO modularity maximization methods to the similarity matrices.

Joint work with Kyung Ha, Grace Li, Blaine Talbut and Thomas Tu from Department of Mathematics, UCLA.